Ferri- and Antiferromagnetic Skyrmion Dynamics

Magnetic skyrmions are topologically stabilized spin configurations that, like domain walls (DWs), can react to external stimuli by collective displacement, which is both physically intriguing and bears promises to realize next generation non-volatile data storage technologies. However, skyrmions in ferromagnets were found to move at an angle with respect to the current direction, which complicates the use of skyrmions in wire devices because the motion component perpendicular to the current can move the skyrmion to a wire edge and thereby annihilate it. Antiferromagnetically coupled systems with compensated angular momentum (antiferromagnetic materials, such as compensated ferrimagnets and natural antiferromagnets) are capable of reducing this effect to zero and could additionally provide high speed dynamics to move DWs at unprecedented speeds. Skyrmions are predicted to move at even higher speeds in these materials, thus making these materials promising candidates for future spintronic devices.

Besides the compensation of perpendicular motion of skyrmions with respect to the drive, the predictability of their trajectories is also of major importance. Analytical equations of motion describe straight 180° DWs in the one-dimensional (1D) model while rigid, circular bubble domains and skyrmions are predicted to move according to the Thiele equation. However, this view has recently been challenged and thus research is required to determine how accurate the commonly applied theoretical models are in different situations.

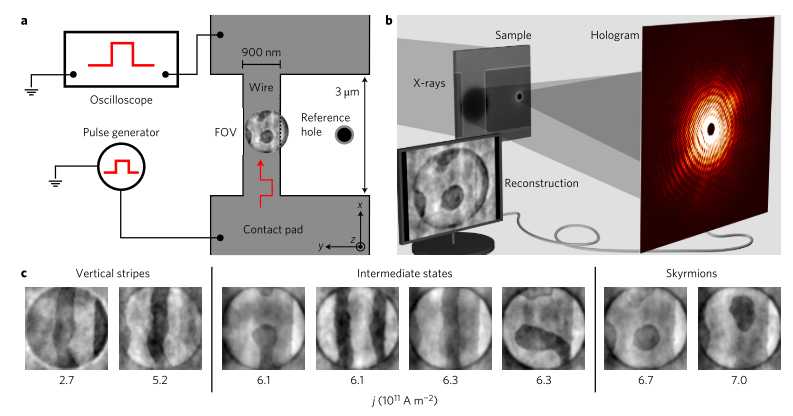
In our group, we study skyrmion dynamics in static and real-time experiments at various large-scale facilities around the globe. The techniques we most commonly use are x-ray holography [1] and x-ray microscopy [2] that can reveal the positions, speeds and shape of spin structures. Most recently, we investigated how strongly deformed DWs and bubble skyrmions move in uncompensated ferrimagnetic Pt/CoGd/W in response to current pulses and found skyrmion speeds in excess of 500 m/s – faster than any other group has reported thus far.

Figure 1: Schematic holography setup. a) current pulses are sent from a pulse generator through the sample device via a series of contacts that were patterned of the device. The transmitted pulse is recorded on an oscilloscope to calculate the current density in the device. B) imaging setup to record the holographical information of the sample. An x-ray beam is sent through a small transparent region of the sample (object hole) and the transmitted light interferes with empty reference holes further away from the probed area. The interference pattern is recorded as a hologram by a CCD camera. The information can be used to reconstruct the magnetic information of the sample device.

Figure 2: (a) Electron micrograph of a typical sample device (dark grey) on a thin silicon nitride membrane (black). Gold contacts on either side are used to inject current pulses. (b) – (g) Examples of distorted domain structures. All displayed bubbles are enclosed domains and are therefore topologically equivalent to a skyrmion. The scalebar in (b) is the same for all subfigures.

Researchers:

Siying, Liza

Recent Publications:

112. E. A. Tremsina and G. S. D. Beach, “Atomistic simulations of distortion-limited high-speed dynamics of antiferromagnetic skyrmions,” Phys. Rev. B, vol. 106, p. L220402 (2022). (view pdf)

102. F. Büttner, B. Pfau, M. Bottcher, M. Schneider, G. Murcurio, C. M. Gunther, P. Hessing, C. Klose, A. Wittmann, K. Gerlinger, L.-M. Kern, C. Struber, C. von K.-S. J. Fuchs, D. Engel, A. Churikova, S. Huang, D. Suzuki, I. Lemesh, M. Huang, L. Caretta, D. Weder, J. H. Gaida, M. Moller, T. R. Harvey, S. Zayko, K. Bagschik, R. Carley, L. Mercadier, J. Schlappa, A. Yaroslavtsev, L. L. Guyarder, N. Gerasimova, A. Schertz, C. Deiter, R. Gort, D. Hickin, J. Zhu, M. Turcato, D. Lomidze, F. Erdinger, A. Castoldi, S. Maffessanti, M. Porro, A. Samartsev, J. Sinova, C. Ropers, J. H. Mentink, B. Dupe, G. S. D. Beach, and S. Eisebitt, “Observation of fluctuation-mediated picosecond nucleation of a topological phase,” Nat. Mater., vol. 20, p. 30-37 (2021). (view pdf)

101. L. Caretta, S.-H. OH, T. Fakhrul, D.-K. Lee, B. H. Lee, S. K. Kim, C. A. Ross, K.-J. Lee, and G. S. D. Beach, “Relativistic kinematics of a magnetic soliton,” Science, vol. 18, p. 1438-1442 (2020). (view pdf)